Matematikai feladvány: kocka testátlója

A számításhoz mindössze egyetlen jól ismert matematikai összefüggést kell használnunk: ez pedig a Pitagorsz-tétel.

Pitagorasz tétele szerint a derékszögű háromszögekre igaz, hogy:

azaz a háromszög két befogójának négyzetének összege egyenlő az átfogó négyzetével.

Na és persze azért nem árt tudni, hogy a kocka felszínét hogyan kell kiszámolni. A kocka felszíne 6 egybevágó négyzet területével egyezik meg. Azaz, ha a kocka élét "a"-val jelöljük, akkor a felszíne: 

A = 6 a²

A példánkban szereplő négyzet oldalát ha "a"-val jelöljük, akkor a négyzet alaplapjának átlója (lapátló) így írható fel (Pitagorasz tétele alapján):

lapátló =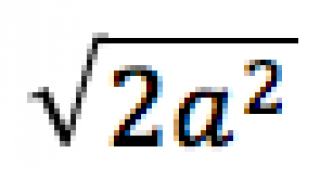 

Ennek ismeretében a kocka belsejében lévő derékszögű háromszögre (melynek átfogója a testátló, egyik befogója a kocka éle, míg a másik befogója a lapátló) is felírható Pitagorasz tétele, melyből:

3 a² = 100

És ebből nem is kell nekünk kiszámítanunk "a" értékét, hiszen nem a kocka élére, hanem annak felszínére vagyunk kíváncsiak a feladatban:

És mivel a felszín: A = 6 a²

így A = 200

A SzámoldKi.hu oldal azzal a céllal jött létre, hogy hasznos kalkulátorokat fejlesszen olvasóinak, melyek segítségével könnyen kiszámolhatnak olyan dolgokat, melyhez komolyabb utánjárás, vagy szakmai háttér szükséges. A kalkulátorokat a főoldalunkon kategóriák szerint csoportosítottuk, de intelligens keresőnk segítségével is könnyen megtalálhatod a Neked szükséges kalkulátort.

Legnépszerűbbek:

Mennyi idő van még hátra az életemből? 

Gyorshajtáskor mennyi a bírság összege?

Mekkora az agyam a magyar átlaghoz viszonyítva?

stb.

A kalkulátorokon túl játékos feladványokat, matematikai kvízeket, gondolkodtató és vicces rejtvényeket is találsz a SzámoldKi.hu oldalán IDE kattintva.